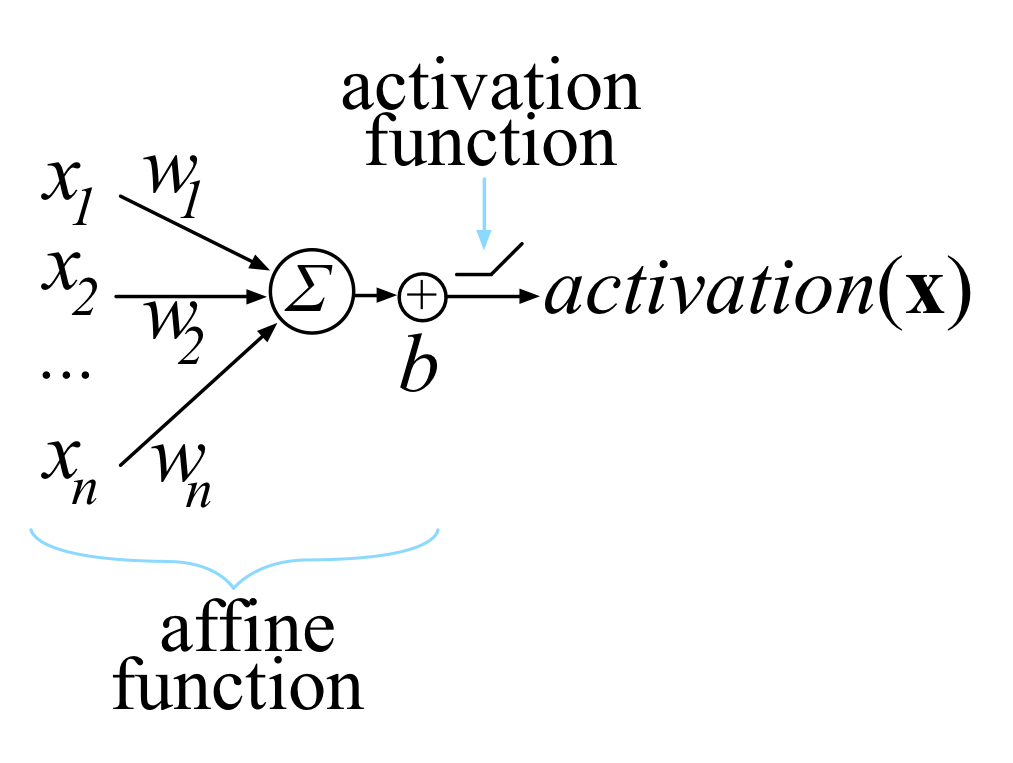
Vector Differential Operator Symbol

When applied to a function defined on a one dimensional domain it denotes its standard derivative as defined in calculus.
Vector differential operator symbol. As a finite dimensional example the subspace of linear transformations of a finite dimensional vector space invariant under the group of unitary transformations. A symbol is just a realization of a differential operator on the cotangent bundle. Del defines the gradient and is used to calculate the curl divergence and laplacian of various. An operator is similar to a function green 1998.
If the coefficients take values in the set of t s dimensional matrices over k then the linear differential operator a is defined on vector valued functions u u1 us and transforms them into vector valued functions v v1 vt. The differential operator del also called nabla operator is an important vector differential operator. The highest order terms of the symbol known as the principal symbol almost completely controls the qualitative behavior of solutions of a partial differential equation. In particular in this connection it leads to the notion of a pseudo differential operator.
A linear partial differential operator is elliptic if it s principal symbol is a linear space isomorphism for all nonzero covector fields omega neq0 in gamma t m. If the symbol were inavariant under some transformation it would restrict the corresponding operator to some subset which may be less interesting. These notions also hold for nonlinear partial differential operators between spaces of sections of vector bundles by considering the operator s linearisation. In this case the principal symbol is the highest degree homogeneous component of the symbol.
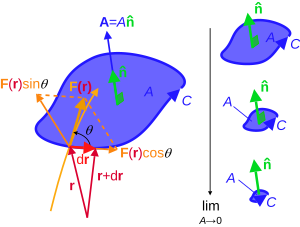
The nabla symbol del or nabla is an operator used in mathematics in particular in vector calculus as a vector differential operator usually represented by the nabla symbol. Generally the symbol of a possibly non linear differential operator is similarly the map on the cotangent bundle given by replacing partial derivatives by covectors in the definition of the differential operator. It appears frequently in physics in places like the differential form of maxwell s equations in three dimensional cartesian coordinates del is defined.